从调用栈溢出到尾递归优化
一、调用栈
前文提过，执行上下文栈（Execution context stack，ECS）也叫函数调用栈(call stack)，以 LIFO（后进先出）栈结构的形式，存储代码执行时创建的执行上下文。
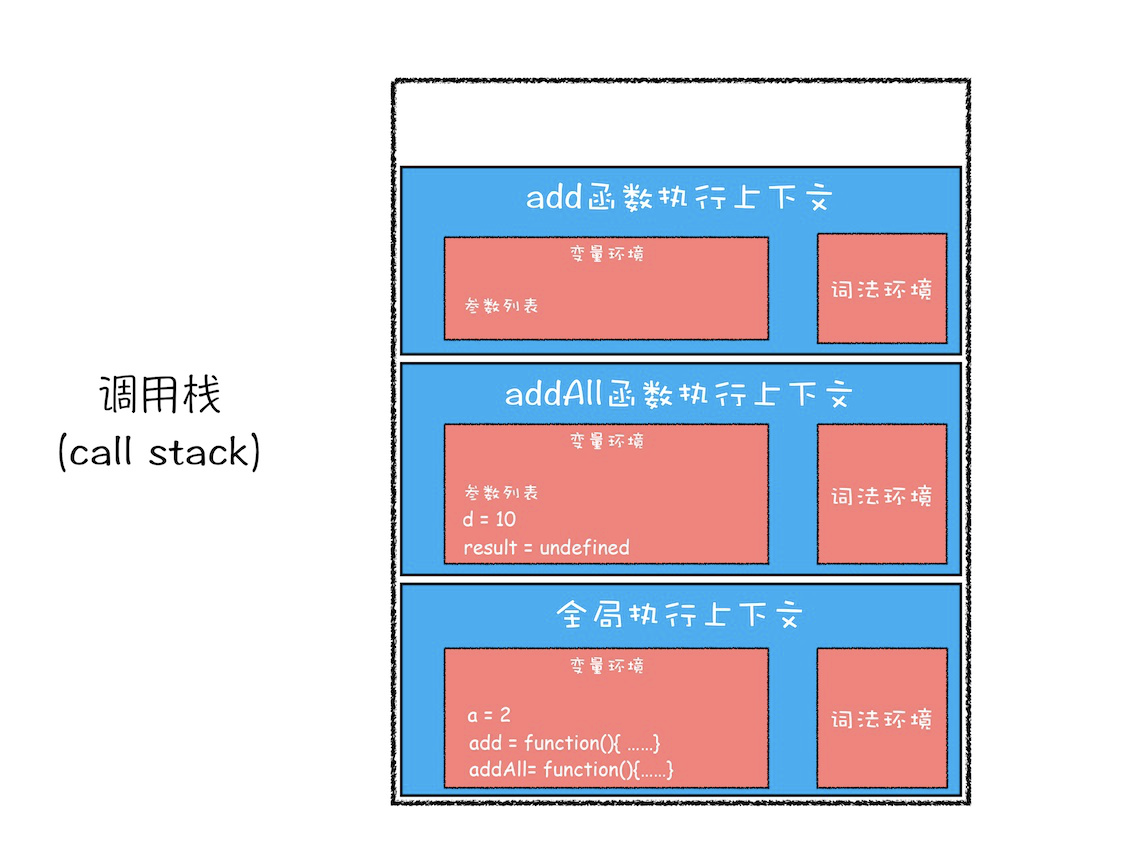
二、栈溢出
调用栈是有大小的，当入栈的执行上下文超过一定数目，JavaScript 引擎就会报错，我们把这种错误叫做栈溢出。
function division(a, b) {
return division(a, b)
}
console.log(division(1, 2))当执行时，就会抛出栈溢出错误，如下图：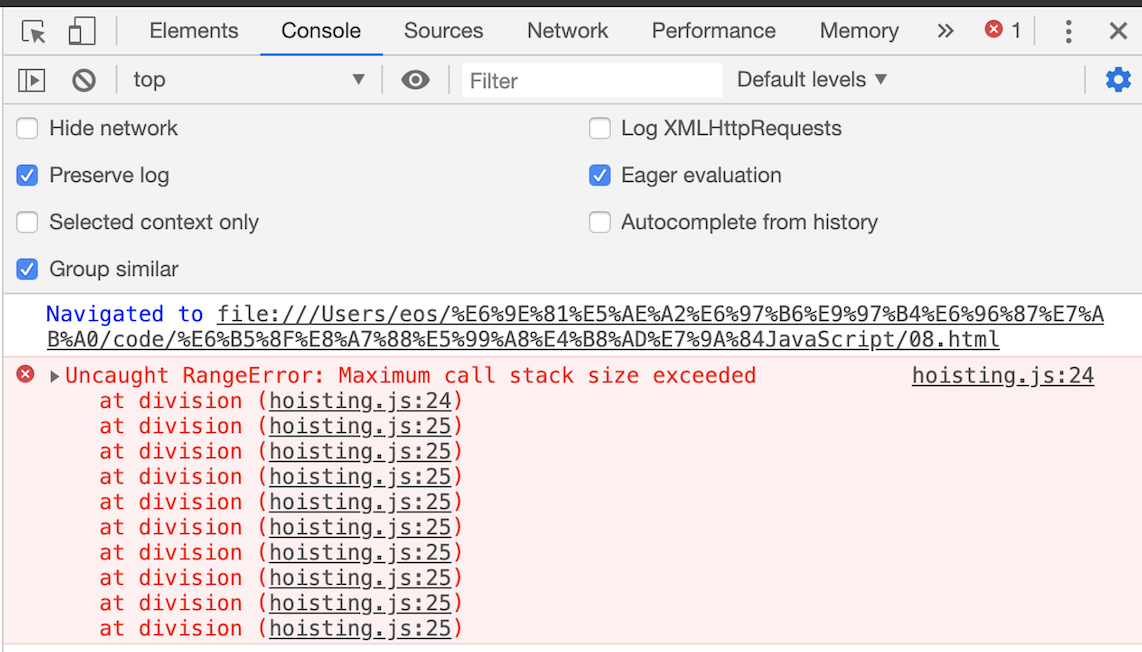 
原因在于 这个函数是递归的，并且没有任何终止条件，所以它会一直创建新的函数执行上下文，并反复将其压入栈中，但栈是有容量限制的，超过最大数量后就会出现栈溢出的错误。
三、什么是尾调用？
尾调用指某个函数的最后一步是调用另一个函数。
function f(x) {
return g(x)
}四、尾调用优化
尾调用之所以与其他调用不同，就在于它的特殊的调用位置。 我们知道，函数调用会在内存形成一个"调用记录"，又称"调用帧"（call frame），保存调用位置和内部变量等信息。如果在函数 A 的内部调用函数 B，那么在 A 的调用记录上方，还会形成一个 B 的调用记录。等到 B 运行结束，将结果返回到 A，B 的调用记录才会消失。如果函数 B 内部还调用函数 C，那就还有一个 C 的调用记录栈，以此类推。所有的调用记录，就形成一个"调用栈"（call stack）。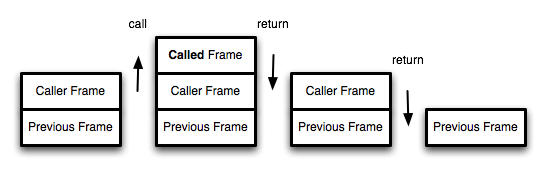 
function f() {
let m = 1
let n = 2
return g(m + n)
}
f()
// 等同于
function f() {
return g(3)
}
f()
// 等同于
g(3)上面代码中，如果函数 g 不是尾调用，函数 f 就需要保存内部变量 m 和 n 的值、g 的调用位置等信息。但由于调用 g 之后，函数 f 就结束了，所以执行到最后一步，完全可以删除 f() 的调用记录，只保留 g(3) 的调用记录。
这就叫做"尾调用优化"（Tail call optimization），即只保留内层函数的调用记录。如果所有函数都是尾调用，那么完全可以做到每次执行时，调用记录只有一项，这将大大节省内存。这就是"尾调用优化"的意义。
尾递归
函数调用自身，称为递归。如果尾调用自身，就称为尾递归。 递归非常耗费内存，因为需要同时保存成千上百个调用记录，很容易发生"栈溢出"错误（stack overflow）。但对于尾递归来说，由于只存在一个调用记录，所以永远不会发生"栈溢出"错误。
function factorial(n) {
if (n === 1) return 1
return n * factorial(n - 1)
}
factorial(5) // 120上面代码是一个阶乘函数，计算 n 的阶乘，最多需要保存 n 个调用记录，复杂度 O(n) 。 如果改写成尾递归，只保留一个调用记录，复杂度 O(1) 。
function factorial(n, total) {
if (n === 1) return total
return factorial(n - 1, n * total)
}
factorial(5, 1) // 120由此可见，"尾调用优化"对递归操作意义重大，所以一些函数式编程语言将其写入了语言规格。ES6 也是如此，第一次明确规定，所有 ECMAScript 的实现，都必须部署"尾调用优化"。这就是说，在 ES6 中，只要使用尾递归，就不会发生栈溢出，相对节省内存。